Why is Fusion Energy so Challenging to Achieve?
By: Derek A. Sutherland, ASP Adjunct Fellow, Seattle, WA.
As a member of the fusion energy research and development community, I find it refreshing to speak with individuals outside my field, and even outside of the scientific research community as a whole to better understand how fusion energy is perceived. Common responses range from a motivating “a cutting-edge energy source that isn’t quite ready yet, but will be soon” to the more cynical “the energy source of the future, and it always will be.” I gravitate towards the positive viewpoint as I know the immense potential of the widespread adoption of fusion energy, and I can readily observe and understand the progress that is continuously being made in this exciting field of scientific research and development.
But, I can also appreciate the skeptical viewpoints of some individuals I have spoken with. From outside of this research community, fusion appears to be an energy source that has not lived up to its potential; a commercial, net-electric fusion reactor does not presently exist. Why has this technology remained elusive? What makes fusion energy so difficult to achieve? When posed with such questions, answers are not as confidently given.
The complexities of plasma physics and fusion energy science are inexhaustibly fascinating in their own right, and there are still unknowns yet to be uncovered and understood. But, when considering the prospect of building a fusion reactor, the fundamental conditions that must be achieved are relatively easy to understand. In a sense, the complexities of fusion energy science regard how to achieve reactor conditions, not what those conditions are. Regardless of how you go about building your working fusion reactor, the fundamental fusion conditions that must be achieved underpin the challenge of fusion energy overall.
One of the central challenges of fusion energy is the temperature required to produce meaningful amounts of fusion power from an ionized gas that is commonly referred to as a plasma. The necessary temperatures for fusion energy production vary depending on the type of fusion being pursued. One of the most popular fusion reactions considered for first generation fusion systems is called deuterium-tritium (DT) fusion. One of the primary reasons for pursuing DT fusion first is that it requires the lowest plasma temperatures to make significant amounts of fusion power when compared to more exotic types of fusion. Even so, the plasma temperatures in the core of an eventual DT fusion reactor will be approximately 150 to 200 million degrees, which is amazingly hot compared to temperatures we encounter in everyday life. These high-temperatures are largely a non-negotiable requirement for fusion in the sense that at substantially lower temperatures, no matter how much fuel you put into the reactor, the amount of fusion power produced will be vanishingly small simply because fusion reactions are not likely to occur at those temperatures.
Assuming a particular plasma temperature in a fusion reactor must be maintained, how do we go about doing so? To begin answering this question, assume that you have a cup of coffee on your desk you would like to maintain at 150 F. If left on its own, the coffee would begin to cool, and continue doing so until it reaches room temperature. The amount of time required for it to cool will depend on how quickly the thermal energy leaks out of the cup into the ambient environment. We know there are ways to extend the time it takes for the coffee to cool, such as putting it in a heat retaining container (e.g. a Styrofoam cup, or a Thermos). But, even when using these thermal insulators, the coffee will eventually cool to room temperature unless we supply energy to the system to keep its temperature at 150 F. A solution for doing so, which also satisfies the everlasting need for caffeine during rainy days in Seattle, is to drink some of your coffee that has cooled slightly below 150 F, and then fill your cup back up with coffee that is warmer than 150 F. With a balance between energy input and output, the coffee temperature can be held nearly constant indefinitely; this thought experiment exemplifies the first law of thermodynamics, otherwise known as conservation of energy.
As simple as this example seems, it captures the salient features of an operating fusion reactor. In this analogy, the temperature of the coffee is to the temperature of the fusion plasma. The rate of leakage of thermal energy out of the coffee cup is called the energy confinement time in a fusion reactor. The warmer coffee that is poured into cup is the energy input into the fusion plasma, which is mostly by charged fusion products (e.g. helium nuclei in DT fusion), and auxiliary heating sources such as microwaves, fast neutral particle beams, or resistive heating from electrical currents flowing in the fusion plasma. All of these energy sources must balance the energy losses from the system to maintain the desired temperatures for fusion to occur. Lastly, the amount of fusion power produced is directly related to plasma density to the second power (e.g. ) while operating at optimal plasma temperature of 150 to 200 million degrees.
Thus, in the previous paragraph we identified three quantities of interest for designing a fusion reactor, the plasma density , the plasma temperature , and the energy confinement time . Using the law of conservation of energy, just like in our caffeine focused example, the result can be expressed as the product of being greater than or equal to a particular number for fusion “ignition” to occur. Fusion ignition is the point when the system becomes self-sustaining from an energy standpoint. This expression is called the “triple product,” which is also colloquially referred to as the “Lawson criterion” by some in the fusion research community today. I argue that this is the most important equation in fusion energy science since it provides the absolute plasma parameters that must be pursued in any fusion reactor system. A commercial fusion system will likely operate below ignition conditions, but it must be close to said parameters to allow for high power “gain,” meaning that significantly more power is produced than is required to keep the fusion reactor operating. The excess fusion power that is produced is ultimately converted into electricity for sale to consumers.
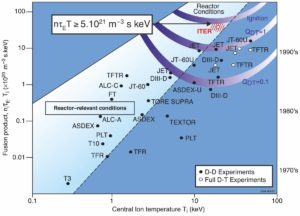
Fusion triple-product performance in various devices over time. Courtesy of EUROfusion
Now, back to our original question: why is fusion energy so challenging to achieve? The simple answer is that it has been particularly difficult to obtain high enough plasma densities , temperatures , and energy confinement times simultaneously for a reactor to approach ignition conditions. In particular, a sufficiently long energy confinement time (e.g. how quickly our fusion plasma (or coffee) cools) has been especially difficult to achieve while simultaneously reaching the temperatures and densities required for meaningful amounts of fusion power to be produced. However, we have made great strides in our understanding of plasma physics over the past decades and have dramatically improved “triple-product” plasma performance, as can be seen in the Fig. 1. Plotted are the maximum values of triple-products obtained in various fusion experiments, and it is clear remarkable progress has been made. The ITER tokamak experiment, presently under construction in Cadarache, France, is slated to be the first fusion reactor to produce more energy than is put in, and by a factor of ten. ITER will mark another meaningful step towards an eventual commercial fusion power plant, and will be the best performing fusion experiment to date on the “triple-product” basis, as shown in Fig. 1.
Now you are armed with the knowledge of the most important equation in fusion energy science, and know what parameters guide the design of fusion reactor systems. So, how have we improved triple-product performance so much over the past decades? And, how do we continue improving it until we produce a commercial fusion reactor system? In my next post, I will begin to address the question of how in more detail.





